電網(wǎng)巡檢機器人的應用在現(xiàn)代電網(wǎng)管理中顯得尤為重要。電網(wǎng)巡檢機器人能夠在顯著提升巡檢效率、減少人工巡檢的煩瑣與耗時的同時,保障巡檢質(zhì)量,通過精準的數(shù)據(jù)采集和處理,降低漏檢和誤檢率。此外,該機器人還能有效應對復雜環(huán)境,減少安全風險。電網(wǎng)巡檢機器人能夠?qū)崿F(xiàn)智能分析,提供數(shù)據(jù)支持決策,優(yōu)化電網(wǎng)運行。因此,關于電網(wǎng)巡檢機器人的研究具有較好的經(jīng)濟效益與廣闊的應用前景,是當前的研究熱點。
本文對巡檢機器人變形底盤傳動齒輪部分進行有限元分析。首先,在Solidworks中完成對變形底盤部分模型的建立;其次,將其導入ANSYS Workbench有限元分析軟件中,對傳動齒輪進行靜力學分析,獲得齒輪在靜力作用下的應力分布、位移變形等重要數(shù)據(jù)。為了驗證有限元分析結(jié)果的準確性,本文還將分析得到的數(shù)據(jù)與赫茲接觸理論的計算結(jié)果進行比對,通過這種綜合應用理論計算與有限元分析的方法,全面、準確地評估齒輪的性能。
1、巡檢機器人底盤部分的三維模型
由于巡檢作業(yè)場景的多樣化與工作環(huán)境的局限性,巡檢機器人采用可以伸縮的變形底盤,其部分三維模型如圖1 所示。底盤的變形主要依賴電機驅(qū)動的雙向絲桿旋轉(zhuǎn)機制。
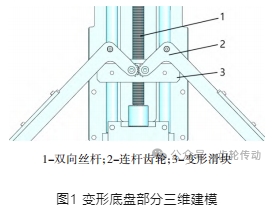
當電機啟動時,它會驅(qū)動絲桿進行旋轉(zhuǎn),絲桿的旋轉(zhuǎn)進而帶動滑塊在絲桿上前后滑動,這種滑動運動帶動連桿齒輪發(fā)生轉(zhuǎn)動,最終轉(zhuǎn)化為底盤的變形動作,實現(xiàn)了底盤的靈活調(diào)整與變換。
2、齒輪參數(shù)和赫茲接觸理論分析
齒輪參數(shù)設計
在本次分析過程中,兩個異形齒輪齒數(shù)為 Z=19(實際為7),齒輪的材料為AISI 304不銹鋼,具體的材料參數(shù)如表1所示。

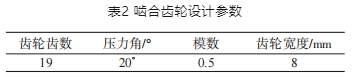
齒輪設計參數(shù)如表2所示。
赫茲接觸理論分析
赫茲接觸方程由德國物理學家海因里希·魯?shù)婪?middot;赫茲在1882年首次提出,在這一理論中,深入探討了彈性體在接觸狀態(tài)下的相互作用。接觸疲勞強度計算公式σH如下。
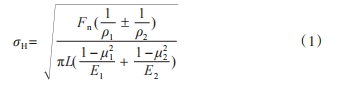
式(1)中:σH為接觸應力;Fn為法向力;±為接觸類型,正號表示正接觸,負號表示負接觸;μ1、μ2為兩種材料的泊松比。
ρε 為綜合曲率半徑,且 ρε = ρ1 ρ2 /(ρ1 ± ρ2 );ZE 為材料彈性系數(shù),![]()
把 ρε 和 ZE代入式(1)中,得到簡化的接觸疲勞強度計算公式σH:
鑒于齒輪在節(jié)點處所受的力和沖擊振動顯著增大,為簡化計算過程,可以將赫茲接觸方程特定地應用于齒輪節(jié)點處的許用應力計算。在進行這種簡化時,需要特別考慮以下幾個關鍵因素:材料的彈性系數(shù)ZE、節(jié)點區(qū)域系數(shù) ZH與齒輪嚙合的重合度系數(shù) Zε。故將復雜的赫茲接觸方程簡化為一個特定于齒輪節(jié)點處的許用應力計算公式,從而更加高效地進行齒輪強度的評估和分析。按照上述簡化,可得:
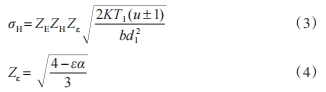
在式(3)和式(4)中:T1為小齒輪所承受的轉(zhuǎn)矩;u 為傳動比,由于兩個齒輪完全相同,則u = 1;d1為小齒輪的分度圓直徑,此處,d1=9.5 mm;b為齒輪的寬度,其數(shù)值為8 mm。
由于齒輪為標準安裝,壓力角為20° ,通過查閱相關資料,得知材料彈性系數(shù) ZE=188,節(jié)點區(qū)域系數(shù) ZH=2.3,通過查表,得重合度系數(shù)Zε=1.1。假設齒輪承受的最大轉(zhuǎn)矩T1=1 000 N·mm,將上述參數(shù)帶入式(3)中,可得σH=260.37 MPa,從而得到理論最大接觸應力為260.37 MPa。
3、嚙合齒輪的有限元靜力學分析
模型的簡化
鑒于齒輪失效的主要形式為齒面接觸和齒根斷裂,齒面和齒根區(qū)域為齒輪中最薄弱且最易受損的重要部分,因此,在進行有限元分析時,這兩個關鍵位置必須保留原始設計細節(jié),以確保分析結(jié)果的準確性。故將嚙合齒輪的三維模型直接導入有限元分析軟件中,確保齒面和齒根區(qū)域的特征得以完整地保留和模擬,這樣可以確保對齒輪性能進行全面且準確的評估。
網(wǎng)格劃分
在對齒輪模型進行有限元分析的網(wǎng)格劃分階段,通常有兩種主要類型的網(wǎng)格可供選擇:四面體網(wǎng)格和六面體網(wǎng)格。雖然六面體網(wǎng)格可能在理論上提供更高的計算精度,但在實際應用中,四面體網(wǎng)格在結(jié)構(gòu)簡化方面的要求較低,且其劃分過程更為高效,因此,選擇使用四面體網(wǎng)格進行劃分。在劃分時,鑒于嚙合接觸的位置對應力分析和接觸力計算至關重要,故對接觸區(qū)域進行單獨的網(wǎng)格加密。具體而言,整體模型的網(wǎng)格精度設定為2 mm,嚙合接觸區(qū)域的網(wǎng)格精度則細化至1 mm,以確保該區(qū)域的計算準確性。網(wǎng)格劃分的結(jié)果如圖2所示。
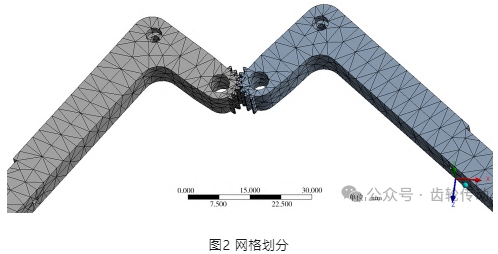
使用四面體網(wǎng)格劃分節(jié)點數(shù)為29 680,單元數(shù)目為16 660。
添加邊界和約束條件
施加載荷以模擬實際工作過程中的受力情況。設定左側(cè)異形齒輪為主動輪,首先給右側(cè)齒輪添加固定副,設定左側(cè)齒輪為旋轉(zhuǎn)副并且施加轉(zhuǎn)矩T1=1 000 N·mm。另外,設置二者接觸類型為摩擦接觸,摩擦系數(shù)為0.1。
求解結(jié)果分析
在完成以上步驟后,求解,得到嚙合齒輪變形云圖、應變云圖,如圖3、圖4所示。
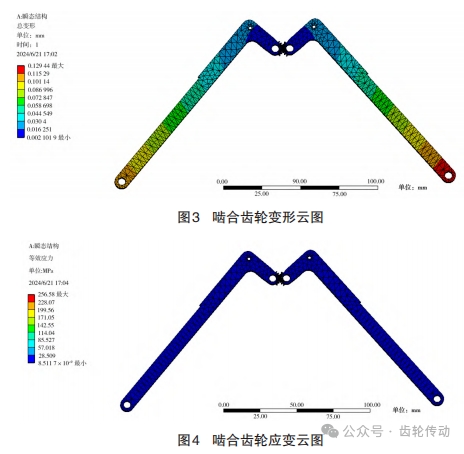
通過分析上述的應力應變云圖,發(fā)現(xiàn)嚙合齒輪在最大載荷下產(chǎn)生的形變僅為0.13 mm,這顯示了該齒輪在工作過程中的形變量極小,從而確保了良好的傳動性能。從分析結(jié)果中看出,在1 000 N·mm的轉(zhuǎn)矩作用下,通過有限元分析得出的接觸應力σH=256.58 MPa,同時利用赫茲接觸理論進行的理論計算得到的接觸應力 σH=260.37 MPa。盡管兩個結(jié)果之間存在微小的差距,但考慮到赫茲接觸計算公式中參數(shù)選取的多樣性和復雜性,這種差距是可以接受的。
4、結(jié)論
(1)經(jīng)過對嚙合齒輪的有限元靜力分析,得出齒根和齒面嚙合處為潛在的高應力區(qū),這些區(qū)域容易發(fā)生失效。因此,在優(yōu)化齒輪設計時,應重點關注齒根和齒面接觸等關鍵部位,以提高齒輪的可靠性和耐用性。
(2)在評估齒輪接觸應力時,傳統(tǒng)的赫茲接觸理論雖然精確,但其計算過程涉及眾多參數(shù)如重合度、載荷系數(shù)等,這不僅煩瑣而且容易出錯。相較之下,利用 ANSYS Workbench進行有限元分析能夠迅速且準確地計算出接觸應力,且與赫茲接觸理論的結(jié)果相近。因此,在效率和準確性方面,有限元分析校核相較于傳統(tǒng)赫茲接觸理論校核具有明顯的優(yōu)勢。通過對嚙合齒輪進行有限元靜力分析,可以發(fā)現(xiàn)變形齒輪的強度和強度滿足使用要求。
參考文獻略.
